Exercices Similitudes  

Exercice 1:

Dans le plan orienté, on considère un triangle OAB direct et rectangle en O.
On désigne par J le milieu de [AB].
M est un point variable de la droite (D) perpendiculaire en A à (AB).
La perpendiculaire en O à (OM) coupe (AB) en M'.

1:Soit s la similitude de centre O telle que s(A)=B.
   a)Montrer que, pour tout point M de (D), s(M)=M'.
   b)En déduire que, lorsque M décrit (D), le triangle OMM' reste semblable à un triangle fixe que l'on précisera.

2: a)Montrer que , pour tout point M de (D), le point I milieu de [MM'] est l'image de M par une similitude S de centre O dont on précisera le rapport et l'angle.
    b)Soit H le projeté orthogonal de O sur (D).Déterminer S(H).
    c)Déterminer le lieu géométrique du point I lorsque M décrit (D).

3: Pour tout point M de (D) distinct de A, on désigne par P le point tel que MAM'P est un rectangle.
    Déterminer le lieu géometrique du point P lorsque M décrit "(D) - {A}".
 

Corrigé

Exercice 2:

Le plan P est rapporté au repère orthonormal direct .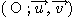
On désigne par T l'application de P dans P qui, à tout point d'affixe z, associe
le point M' d'affixe z' =(1 + i)z - i.
1: Montrer que T est une similitude directe de P don't on donnera les élèments caractéristiques
   On notera A le point invariant de T.
   Donner une mesure de l'angle , en supposant que M A.

2: a) Construire M' pour un point M donné.
    b) Déterminer l'image de D' par T de la droite D d'équation y = x.
        Construire D'.

3: a) Montrer qu'il existe un point B du plan distinct de A et un seul tel que les
        affixes z₀ de B et z'₀ de B' = T(B) soient liées par la relation z₀z'₀=1.
        Mettre en place B et B'.
     b) Soit A' le symétrique de A par rapport à O.
         Montrer que les points A, A' , B et B' sont cocycliques.

Corrigé

Exercice 3: Bac S Juin 98 (Spécialité)

Dans le plan orienté , une unité étant choise, on considère un rectangle ABCD tel que
.
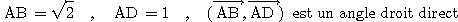I désigne le milieu de [AB].
Partie A:
Soit (E) l'ensemble des points M du plan tels que MD² - MB² =1.
1: Vérifier que les points C et I appartiennent à (E).
2: a) Déterminer et construire (E).
    b) En déduire que les droites (BD) et (CI) sont perpendiculaires.

Partie B:
Le plan est rapporté au repère orthonormal direct
 Soit S une similitude directe qui, au point M d'affize z , associe le point M' d'affixe z' telle que:
 z' = az + b , où a et b sont des nombres complexes avec a non nul.
1: Déterminer les nombres complexes a et b pour que S(D) =C et S(C) = B.
2: Soit T la similitude directe qui, au point M d'affixe z , associe le point M' d'affixe z' telle que:
               
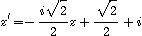
    Déterminer le rapport et l'angle de T.
3: Montrer que la similitude T transforme B en I.
4: En déduire une autre justification de l'orthogonalité des droites (BD) et (CI).
5: Montrer que le centre W de la similitude T est le point d'intersection des droites (BD) et (CI).

Corrigé

RETOUR